It is a common misconception that the very concept of music possesses some sort of universal laws that govern how it works and that these laws are applicable to how music works all around the world, in all musical cultures.

The tired argument goes that with the help of the harmonic series, we can mathematically determine which harmonies and melodies sound the 'best' together and that all human brains from all cultures around the world will perceive certain intervals as 'more stable' and some as 'less stable' as some sort of universal constant.

The claim that the harmonic series is responsible for our specifically western idea of musical consonance and dissonance is not entirely unfounded, however, to say that it is the chief governing factor behind all music, all around the globe, is just silly. The cultural decision on what tuning system to use is an artistic decision, not a mathematical decision. A decision that different cultures around the world have made in very different ways.

The terms "tension" and "resolution" and "consonance" and "dissonance" are especially culturally learned. Cultures foreign to us use sounds that, to our ears. sound "tense", but these sounds are completely normal and resolved to them. That's because they're simply used to hearing those sounds, and in a different context than we are. It simply does not possess the same cultural connotation as we have. I wouldn't be surprised if there are musical cultures out there that do not even possess a concept of "tension" and "resolution in their systems. Or at least didn't previously possess these concepts before colonization.

Several academic research studies, as well as examples of global musical tradition, point towards the answer lying within our instruments themselves. We will explore different musical cultures, their tuning systems, and eventually we will look at examples of how the harmonic characteristics of instruments have led to the tuning systems used by those cultures. Finally, we will look at how we can use these findings can help us come to a conclusion on how our ideas of consonance and dissonance have come to be.

The Harmonic Series, in short

When a note is played, it's physical sound wave vibrates at it's whole wavelength, as well as half of it, and as a third of it and so on and so on. This creates a series of harmonics, which are extra notes that ring out in addition to the note we are playing, albeit at a far less audible volume. This set of harmonics is called the Harmonic Series, or the Overtone Series.

The Harmonic series is comprised of two parts. The initial note that is played, and its harmonics.

The initial note that is played is called the fundamental frequency. This is also the note that is recognized by the human ear as the note that is being played. If you play a C4 note on your piano, that C4 (which has a frequency of 261.6 Hz) is your fundamental frequency.

Then, we have the rest of them. These are all those harmonics that play in addition to our fundamental frequency. These are our Harmonic Frequencies. They are integer multiples of our fundamental frequency. Let's explore how that works. These are sometimes known as partials.

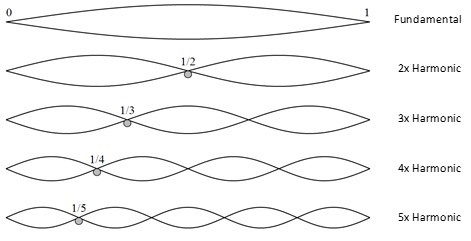
In order to build our harmonic series, we simply add them up. If our fundamental is a low A1 note, at 55 Hz, we will add it to itself (55 + 55) to get our first harmonic, the octave. This gives us 110hz, which is indeed an A2 note. Then, we will continue to add 55 on to each fundamental to get the series!

This yields 55hz, 110hz, 165hz, 220hz, 275hz, 330hz, 385hz, 440hz, 495hz, and so on and so on to infinity. You can see this logarithmic sequence displayed best by pure string harmonics, which you can see pictured.

If we were to roughly map this out as a scale, we would go up by an Octave, Fifth, Fourth, Major third, Minor Third, and so on.

You might have noticed as well, you can simply multiply the fundamental by whichever harmonic you want to get. So, 55 x 5 gives us 275, which is indeed our fifth harmonic.

The harmonic series is an additive series. This means that when you play a lower note, it's going to sound more harmonically complex and acoustically busy than playing a higher note would. Humans can only hear so high, so it stops for us eventually. Each partial above the fundamental is significantly quieter than the fundamental. The lower the fundamental, the more audible the overtones are, which is why low frequencies can sometimes sound very muddy, but at other times quite rich.

Interestingly enough, this is one of the primary factors that shapes timbre in music, which is just a fancy word for 'how an instrument sounds'. The way a piano sounds different than a Flute.

Now, this is all pretty interesting, but how does it relate to consonance and dissonance? The claim goes that our tuning system and the consonances and dissonances we find within it are intrinsic to our brains because it's our brains "doing math" with the harmonic series. Just because the math sounds good though, does not yield enough weight to claim that it's behind all harmony and melody in music. What makes music sound good isn't just your brain subconsciously doing math or something silly like that.

The McDermott Studies

Indifference to dissonance in native Amazonians reveals cultural variation in music perception

Just because we have identified scientific principles which may or may not be the reason behind why we enjoy western tonal music, does not mean this is the case globally. The perception of octave equivalence and even the octave itself as being consonant in a musical context is not a universal experience, and is likely a culturally learned phenomena, not pretty looking mathematics.

Dr. Josh McDermott, a Doctor of Brain and Cognitive Sciences at MIT conducted two studies on this subject. One in 2016, focusing on consonance and dissonance, and one in 2019 expanding on the 2016 study, as well as focusing on pitch perception and emotional association in music.

Mcdermott et al. (2016) conducted a myriad studies on the perception of consonance and dissonance in music, utilizing members of an isolated indigenous group located in the Bolivian Amazon, the Tsimane, who have had practically no exposure to western tonal music, or the western tuning system, and found that their preference for consonance and dissonance was not similar to that of people who have been culturally exposed to the western tonal system their entire lives.

In addition to the Tismane people, they also studied comparison populations within the United States and Bolivia, which varied in exposure to Western music.

Participants rated the pleasantness of sounds. Despite exhibiting acoustic discrimination abilities similar to those seen in the west and aesthetic responses similar to those seen in the west in response to familiar sounds and acoustic roughness, the Tsimane’ rated consonant and dissonant chords and vocal harmonies as equally pleasant to their ears.

In addition, McDermott (2019) found that ideas such as major and minor's association with happiness/brightness and sadness/darkness are also completely culturally learned. They also found that octave equivalence is indeed not a universal phenomena, as the Tismane do not possess this concept.

In short, our non-western participants showed no preference for harmonies that we consider consonant in the west (the octave, perfect fifths, perfect fourths, major chords, etc.) over harmonies that are considered dissonant (the tritone, diminished chords, minor seconds, etc.).

Contrasting the findings with the Tsimane, both city and town dwelling Bolivians exhibited a preferences towards the western ideas of consonance, but, to a noticeably lesser degree than US residents. Given that Bolivia was a Spanish colony for about 300 years, it's no mystery why these acoustic preferences have found their way into mainstream Bolivian musical culture.

These results indicate to us that preferences for consonance and dissonance can be absent within cultures that are sufficiently isolated from Western music, and are thus unlikely to reflect innate human biases. The observed variation in acoustic preferences is presumed to be determined simply by environmental exposure to musical harmony. This suggests that the perception of consonance and dissonance is a culturally derived phenomena, and not one that is related to the physical properties of the harmonies and their sound waves.

The study also suggests that these predispositions may be influenced by the construction of the instruments being used, such as the harmonics derived from a string instrument. This is perhaps one of the most important findings of this study.

Gamelan Music

Pelog and Slendro

Indigenous tribes isolated within the Amazon Rainforest are not the only example of this, however. Gamelan music is a traditional style of music played by various Indonesian ethnic groups. There are two musical scales that instruments are tuned to within gamelan music. Pelog and Slendro. Pelog is a newer 7-note scale, from which 5 notes will be selected to be the primary tones for the ensemble, as most gamelan instruments have 5 keys. Slendro is the much, much older 5 note scale, which is a bit more commonly used.

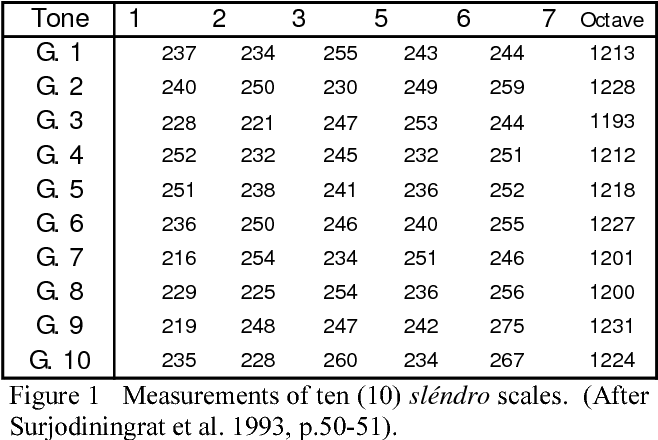
Tuning within gamelan music, however, varies widely from ethnic group to ethnic group as well as from island to island and even from village to village. Slendro is roughly equivalent to 5-tone equal temperament (meaning it divides the octave into 5 notes, however it only roughly fits this classification). The closest approximation that has ever been made for pelog was found in Surjodiningrat (1972), which found a statistical preference towards 9-tone equal temperament, and suggests pelog as a 7 tone subset of this tuning system. However this is just a statistical preference, as the exact intervals between these 5 or 7 notes vary quite a bit, as previously mentioned and this is only really true within the main octave. Slendro and Pelog are commonly only recognized as merely bearing similarities to equal temperaments.

Most gamelans tune the intervals between each of their instruments pretty close together. However, Balinese gamelan intentionally play their instruments in pairs, which are slightly tuned apart in order to produce interference beating when played at a consistent speed for all pairs of notes. This gives their ensembles a very "shimmery" and "busy" timbre made to evoke a feeling of god being present and acting as a catalyst for a meditative state.

This concept also produces stretched octaves, which means that gamelan has the concept of octave equivalence, however they do not follow the western conception of a "pure octave", in which the octave relationship must be a 2:1 ratio, otherwise it is not considered an octave. These octaves can stretch up to as large as greater than a third of a semitone larger than a standard octave. This shatters the conception of the octave that is derived form the harmonic series as being a scientific law of music.

Instruments that do not need to use fixed pitches sometimes insert up to 17 additional pitches into the scale, similar to the microtonal adjustments found in Shruti, a similar concept found in Indian Classical Music.

With all of these complexities, none of them sounds "out of tune" to the people who create and perform this music, as it may for many western listeners.

Creating Alien Music

Even self-constructed musical cultures can be too weird for the West

A real world example comes from the movie Avatar (2009). Director James Cameron wanted to develop a musical culture for the alien species in the film that would feel truly unique and alien to western audiences. So, composer James Horner brought ethnomusicologist Dr. Wanda Bryant aboard to help conjure up some interesting and alien tones for the soundtrack. Together, they put together all kinds of different sounds from all over the world with the aim of fusing them together in such a way that they could create something very unusual that would pass as a genuinely alien musical culture.

Cameron ended up throwing almost all of it out because, in his words, "it was all too fucking weird".

In the realm of Hollywood, when creatives try and create music that sounds like it came from an alien musical culture, inspired by real-world human music (that millions of people enjoy and listen to), they dislike it because in their mind their audience (mostly western) won't be receptive to it. And that's just human music, let alone music that comes from actual aliens. Music is a much broader field than we think it is.

Additional Tuning Examples

From Africa to Asia to Across the Globe

A few other examples of tunings found around the world, which do not derive from the harmonic series, include the following.

In David Morton's 1974 book, The Traditional Music of Thailand, he describes the Thai tuning system which utilizes a tuning of seven nearly equal steps to the octave. This roughly fits into 7-tone equal temperament, however tunings can vary quite a bit.

The five equal-step octave of the 8 string Ugandan harp that was documented by Wachsmann (1950) is a form of 5-tone equal temperament. Interestingly, the music played with this harp shows little regard for fourths and fifths and instead focuses on seconds and thirds. Wachsmann also notes that Ugandan xylophone music uses this same system of tuning, which was later measured and documented by Haddon (1952). Wachsmann later went on to study Ugandan tuning in even more detail in Wachsmann (1952) and documented wide tetratonic tunings, tunings that approximate 5-tet and tunings that approximate heptatonic tunings. He even talks about how using 'cents' is a bad way to look at outside musical cultures, and we should look at them from within and judge them based on the range of values that their writers and performers produce. I highly encourage a read of Wachsmann's 1952 paper, it's very, very progressive and forward thinking for a British guy in the 1950s and even for today.

Measurements of intervals in pre-instrumental Indigenous South American music show equal steps of 175 cents, which result in a stretched octave, similar to that seen in gamelan music. (Boilès, 1969).

Many forms of Kulintang, Southeast Asian gong ensembles, organize their pitch sets without any set tuning, typically arranging their gongs by size of gong, with great variation existing between different ensembles. Many Kulintang do not even consider the concept of scale, instead emphasizing "rhythmic modes". A study by Issac Jimenez was done to further study the role of scale and tuning, among other characteristics of Kulintang music. He concluded that "Kulintang does not have a fixed tuning therefore tonal scale is not relevant in order to write its music" and goes on to further note that "tuning is not relevant as far as kulintang targets to create a melody with the rhythm as the main musical achievement". He concludes that "To be in tune must be a secondary issue".

Angklung, a traditional instrument of West Java, uses variations of Pelog, in addition to three other scales, Madenda, Salendro and Degung. An acoustic analysis by A. S. Sudarsono has shown that all four are 5 note tunings that do not line up with any existing known tunings.

If you go out and buy a "Native American flute", you will get a flute tuned to the minor pentatonic scale, however, this was not practiced until the late 1970s to early 1980s. Up until this time, instruments were most commonly tuned for the individual player's body measurements, so specific tunings weren't very common, however, a couple traditional scales still remain among their people. Traditionally, Indigenous Americans of the Greats Plains and other indigenous groups tuned their flutes to a hexatonic scale consisting of the intervals W h W W W m3. It has been referred to as the North American Indigenous (NAI) scale by contemporary practitioners. The Anasazi, the Ancestral Puebloans, tuned their flutes to a hexatonic scale consisting of the intervals W h h m3 W W h. It has been referred to as the Anasazi scale by contemporary practitioners.

The Harmonic Series and Western Tuning

It doesen't even line up with western tuning systems

Remember how we discussed the Harmonic Series and how harmonics build on top of our fundamental frequency and that's how we can get all the intervals we know and love from it? Well, that's not entirely true. The math doesn't even really apply to our music, at least, not anymore.

The origins of western tuning is commonly recognized as beginning with Pythagorean tuning. It builds a twelve-tone scale involving ratios exclusively of powers of 2 and 3, derived from harmonics found high in the harmonic sequence, creating a sequence of fourths and fifths (which are inversions of each other). An identical system is found in ancient Chinese music, known as Shi-er-lu.

However, stacking fifths in this way, in either direction, does not lead to a perfect octave. The perfect fifth is a ratio of 3/2, while an octave is a ratio of 2/1. If we take 3/2 to the power of 12, the result of 12 successive intervals of a fifth, is not the same as 2 to the power of 7, the result of 7 successive octave intervals. It's not incredibly far off, however it is noticeable. It's about a quarter of a semitone off. So, the Ancient Greeks invented a little hack for this, they called the Pythagorean comma. It adds an extra interval between two enharmonic notes (such as C and B#). This fixed the issue with octaves, but led to instruments being limited to playing in a single key and even limited the chords that you could use within that key, which is why you really never see chords such as A♭ or Fm chords in early music. Chinese musicians and mathematicians recognized this issue around the same time and devised a similar solution.

As thirds became viewed as consonant and the desire for composers to use triads as well as to switch keys grew, there have been many hacks and solutions proposed over the millennia, such as meantone temperament, well temperament, the Ptolemaic sequence and five-limit tuning (which Indian classical music still uses a variation of). Gioseffo Zarlino created the first justly intonated 7-tone (diatonic) scale, which contained pure perfect fifths (3:2), pure major thirds, and pure minor thirds, using the formula of R + M3 + m3 + M3 + m3 + M3 + m3.

These are all tunings known as Justly intonated tunings, which are tunings that use ratios to derive its intervals.

There lies a fundamental conflict between art and math. You just can't have perfect octaves and true perfect fourths both in a system together. Most of the history of western tunings has been designed to work around this issue.

The solution we have come up with is a 12-tone equally tempered tuning, in which we split the octave up into 12 equal intervals. It has a perfect octave and a perfect fifth that is kind of smooshed down a bit so it all fits together fine, since it's only a little off, right?

While the octave, fifths and fourths remain moderately similar to just intonation, 3rds and 6ths are noticeably farther away, yet we still perceive them as consonances. 3rds started to become recognized as consonances around the Middle Ages in Europe, far before this tuning system was invented. Even with the very nature of what a third is, having been changed, by a non negligible amount at that, thirds were still recognized as thirds and seen as consonant despite now being 13-15 cents "out of tune". A challenge that comes with 12-tet is imperfect thirds, but as Europe changed over to equal temperament, it also changed the music that it wrote in order to accommodate the system and to "keep thirds consonant".

The switch to 12-tet gave us access to techniques such as chromatic modulation, maximally smooth voice leading, transpositional equivalency and a keyboard that works well in any key!

The harmonic series may have perhaps had influence on the origins of western tonality, consonance and dissonance, however it is certainly not a universal law, even in western music today. Beyond the 9th harmonic, the harmonic series isn't really much of a guide to consonance. The 11th harmonic is right there in between the perfect and the augmented 11th. The 13th harmonic is 40 cents sharp of the minor 6th - 60 cents flat of a major 6th. Even the 7th harmonic is about 31 cents off.

The 'Just Noticeable Difference' (the amount of cents different a note played consecutively after another note must be for the human ear to recognize that it is different) is about 5 cents (which is 1/20th of a semitone). Within the harmonic series, if we take the first 31 harmonics and compare them to 12TET, 13 of them are less than 5 cents off. However, 18 of them are more than 5 cents. Some of them are a lot more than 5 cents, for example, the 31st harmonic is a major seventh that is 45 cents sharp. Almost half of a semitone!

Our ideas of consonance and dissonance really haven't been a hard science for most of our musical history. Western music has a long history of consonances and dissonances shifting, such as the previous example of thirds.

In some modern forms of music, such as blues, dominant 7 chords are not considered dissonant, and are considered places of rest, consonances, in the music. In some forms of metal and punk music, even the tritone can be considered a point of rest that does not need a resolution, when voiced R - b5 - P8 (I've also heard this called a sus(b5) chord). Examples of this are especially common in the 'mathcore' subgenre.

It's even been argued that a 19-tet scale would be more "mathematically sound" than the 12-tet scale that we use. If the math lines up better, and the math determines what sounds "good" or not, why didn't we gravitate towards 19-tet? There are numerous equally tempered tunings out there, who are we to claim that 12-tet is the only legitimate one, simply because it's the one we use? There's a litany of alternate tunings out there to explore, even if you just relegate yourself to equal temperaments. Check out Xenharmonic Wiki, it's an incredibly robust resource on alternate tunings, how they work and even guides on dipping your toes in on how to play within them and on how harmony moves within them.

Given the advantages of equally tempered tunings and how far they can diverge from the "natural" justly intonated tunings, it does not appear that the harmonic series is an intrinsic law of harmony. But, even if it's not intrinsic to all music, that doesn't mean it can't be of historical importance to how we understand harmony, consonance and dissonance. The octave, fifth and fourth are still really important to a lot of music, including our own, so where did that arise from?

String Harmonics

The answers to our questions lie within the strings

It all comes from string harmonics! Well, not all of it of course, but i think this is a pretty solid hypothesis on the origins of tuning used in musical cultures that are either pentatonic based or are heavily influenced by pentatonic scales, which is a lot of them!

Just because harmony, consonance and dissonance are not concepts intrinsic to the human mind, placed there by the harmonic series, does not mean that the harmonic series has not influenced our idea of consonance and dissonance in more organic and materialist ways.

It isn't difficult to imagine that some of the earliest musical instruments were stringed instruments, such as a hunting bow adapted for musical performance. Stringed instruments are relatively simple to create. Take a string, stretch it between two posts and voila! You have a monochord. One of the world's earliest instruments.

Just plucking away at a single note isn't incredibly interesting, however. So, you can play the harmonics of the string by dividing the string into 1/2, then 1/3, then 1/4, then 1/5 and so on and so on. This is made easy by not requiring a finger board to pla.

When you add other strings, it's not very hard to get a consistent tuning between your strings, if you use one of the harmonics.

When dividing it up, you get the following harmonics.

• First Harmonic - Divided in Half - Octave
• Second Harmonic - Divided in Three - Perfect Fifth
• Third Harmonic - Divided in Four - Perfect Forth
• Fourth Harmonic - Divided in Five - Major Third

This gives us our root, an octave, a perfect fifth, a perfect forth and a major third. A justly intonated major pentatonic scale! Effectively giving us the basis for our modern idea of consonance.

I know what you're thinking. "But didn't you just explain why the harmonic series isn't the root of consonance and dissonance"? And the answer is no, i didn't, i simply tried to explain that it is not a universal phenomena. I'm not discounting the influence it has had on western music and even Anhemitonic pentatonic based harmony in general.

This is probably something that happened in prehistoric music, most likely before humans even spread out all across the globe, or shortly there after.

The instruments you play will, of course, affect how you sing. This means that as string instruments were spread around various tribes and eventually around the globe as those people did, this idea of "consonance" was spread with it. As a result of this, it became ingrained within culture and has continued to be passed down through generations upon generations, from parents singing to their children, those children growing up and singing those same tunes to their children, and so on. This idea of consonance and dissonance has been embedded within us from a young age. This inevitably ends up influencing the creation of other similar instruments and spreading this idea further from there.

Anyone who is a fan of extreme music, such as punk, metal or even noise music, will tell you that this is obvious. When you first begin to listen to extreme forms of metal or noise, such as black metal, or harsh noise rock, the music initially sounds pretty dissonant and non-harmonic. However, as you listen to it more and more, over time, your tastes will change and those dissonances and "non-harmonic" sounds will start to sound "right" to your ears.

The instruments of a culture, especially it's oldest ones, greatly influence tuning, consonance and dissonance. We've already observed this phenomena in Australian Aboriginal culture (aerophone) as well as Indonesian gamelan music (metallophone), so it's not far fetched to apply this same logic to Anhemitonic pentatonic-based tunings and tonality, especially given the prolifically of strings in those cultures.

Evidence for this can be found, particularly in traditional Chinese music. The guqin, a Chinese plucked string instrument that is also one of the oldest known string instruments, is traditionally tuned based off of harmonic overtone positions on the string. The dots on the soundboard indicate the harmonic positions: 1⁄8, 1⁄6, 1⁄5, 1⁄4, 1⁄3, 2⁄5, 1⁄2, 3⁄5, 2⁄3, 3⁄4, 4⁄5, 5⁄6, 7⁄8. This yields a pentatonic scale in multiple different octaves!

In addition, Mesopotamian lyres and harps have been found while excavating the ancient city state of Ur, dated to around 2500 BCE, as well as nearly half a million cuneiform tablets dating to around 1800 BCE. We learned from these findings that the ancient Mesopotamians had a standardized tuning system that was fundamentally identical to the seven ancient Greek scales, which dates 1400 years earlier than the ancient Greek scales, at their absolute latest. Especially interesting is that they derived their nomenclature from the interval of a fourth/fifth on which the tuning procedure starts.

This makes it easy to hypothesize that the Ancient Greeks learned Mesopotamian music theory from the Near East, as they did with mathematics, especially since the lyre and even the monochord itself appears to predate Ancient Greek and was most likely introduced to them by these very same Near East cultures. The historical record itself even shows that Pythagoras himself "reinvented" the monochord from Sumerian writings of the time.

The origins of how music has been and (still is) taught can be traced to this period as well. Sometime after musical tuning derived from string harmonics was introduced to the Greeks from the Near East, there was a division between Ancient Greek music theorists (Baysal 2015). The Pythagorean and Aristoxenian theories. Aristoxerus argued that musical 'science' was based dominantly upon melody, with little to do with mathematics, additionally basing a lot of his theory on texture and dynamics. He was discredited as a "man without reason" by Pythagoras and his followers, men who held mathematics as the core of their epistemology.

Baysal says that "the treatise 'Division of the Monochord' was an instrumental document in this false understanding and rather acted as Pythagorean propaganda in this process." It is a treatise rife with logical error, in which almost all later prepositions would be built upon. Not only that, but he goes on to say that "since the utilization of the monochord has been taught along with the theoretical framework the treatise presented, this new pedagogical and musico-scientific technology would be supporting the Pythagorean argument that it was derived from. Taken in this respect, the monochord becomes the perfect example for Heidegger’s notion of tekhne, as it allows the revelation of “truth” to its user. However this false “truth” is actually a Pythagorean design."

Pythagorean thought eschewed much of the artistry in music in favor of finding 'mathematical reason' within music. This is a fatal logical error, given music is a form of art, not merely an abstraction of acoustic science. This flawed method of thought has since been disguised as a universal truth in music and has consequently been used to uphold some rather reprehensible beliefs in the last couple hundred years, hiding behind a guise of false science.

It is undeniable that the monochord, the most fundamental string instrument in the development of musical history, was instrumental to the music of one of the oldest known civilizations in the fertile crescent, as well as one of the most ancient European civilizations. We also saw its influence in the each with the guqin. We have also found evidence of it being initially tuned/played using its natural overtone series, leading to other instruments being tuned in that manner, and then music theory being taught in a purely 'scientific' manner using those instruments and tuning systems. This has led to a continuous feedback loop of how instruments are made/tuned and how the music to be played on them is composed, therefore effecting general musical composition, and then the development of new instruments, and the cycle continues.

Conclusion

I think the history of why any tuning came to be is best answered with a question. What is it that this tuning system allows this culture to do?

There is a dialectical and material relationship between the music we play and the instruments we play it on. They are bound to each other. One cannot exist without the other, and they are always effecting and changing each other, and they are always in a continuous state of change.

There are several musical cultures around the world that eschew the notion that string harmonics providing a guiding framework for consonance and dissonance, and even topics we see as fundamental as the octave or the fifth! And those are just the musical traditions that have endured and survived hundreds of years of colonialism and imperialism.

Even our western idea of "proper tuning" has changed quite a lot over the past millennia or two. It's because there is no such thing as 'proper tuning'; Simply just the tuning that works best for the instruments that a specific style of music is being played on, and the music that is being played by those instruments.

The notion that the overtone series is responsible for "music sounding good" is an interesting claim, however, it's more musical numerology than it is music theory, and it is directly contradicted by research in psychoacoustics and music psychology, as we have seen.

The seemingly "obvious" universality of the western tonal system around the globe is a product of imperialism, rather than scientific law. Even rejecting that philosophy, it's undeniable how western tuning has evolved to such a degree as it has over the past couple of millennia, and how our ideas of consonance and dissonance have changed with them and vice versa.

It also does not help that a seminal piece of western music theory declared the harmonic characteristics of the monochord musical law and the majority of his successors took this and ran with it, claiming that it was the answer to why music sounds good, and latching onto the false premise that if we just look at the math, derived from one type of instrument, then we can truly understand music!

It's important to note that Australian Aboriginal peoples did not develop the bow and arrow, and consequently did not develop any stringed instruments. Coupled with the previously mentioned study on how Aboriginal musical cultures base their tuning on the harmonics of the didgeridoo, and how Indonesian cultures, who primarily use gongs and percussion in their music, base their tunings off of the harmonics of metallophones common in their ensembles, this theory of string harmonics and western tonality starts to make even more sense.

We have seen that the traditional tuning system of one of the oldest known string instruments is derived from harmonic overtone positions on the string. We have also seen that there is significant evidence to show that the tuning systems and scales that have been used around the world by various musical cultures were based on the harmonics and inharmonic overtones of aerophones and metallophones that were native to their respective cultures. This makes a strong argument that the theory that string harmonics are responsible for our ideas of consonance and dissonance, and certainly lays to rest the argument that consonance and dissonance are derived from string harmonics.

Further Reading (And Watching)

Other fantastic articles (and videos) on similar subjects

• Is Music a Universal Language? by Dr. Linda Shaver-Gleason
• Music is not a universal language and this klezmer song proves it by Dr. Ethan Hein
• Music Theory and White Supremacy by Adam Neely